[最も欲しかった] p(x y) conditional probability 174705-P(x y) conditional probability

Probability density function given that the random variable X is greater than or equal to x is found by rescaling f X X≥x(w)= λe−λw e−λx =λe−λ(w−x) w >x This conditional distribution, if shifted x units to the left, is identical to the original exponential(λ) distribution2) The probability of (A given B) and C ie ## p(A B) \cap C ## I was also wondering if there was an intuitive way to understand how to break it down, but I should probably try to understand this firstBrowse other questions tagged probability conditionalprobability weibulldistribution or ask your own question Featured on Meta Should we replace the "data set request" with distinct "this is an offtopic

Ppt Joint Distribution Of Two Or More Random Variables Powerpoint Presentation Id 2398

P(x y) conditional probability

P(x y) conditional probability-\( 70xy = 1\) which gives \( x y = 50 \) Let event S product selected is a software product , let event H product selected is a hardware product Let event A product selected is from company A , let event B product selected is from company B We are asked to find the conditional probability \( P(HB) \)And what's so cool about conditional probability is that it's not limited to sample spaces with equally likely outcomes In other words, this means that the probability of observing events B and A is the probability of observing A, multiplied by the probability of observing B, given that you have observed A

Null Null Manualzz

• Jointprobabilitymassfunction PX,Y (x,y)=P(X = x,Y =y) • The probability of event {(X,Y)∈ B} is P(B)= X (x,y)∈B PX,Y (x,y) – Two coins, one fair, the other twoheaded A randomly chooses one and B takes the other X = ˆ 1 A gets head 0 A gets tail Y = ˆ 1 B gets head 0 B gets tail Find P(X ≥ Y) • Marginal probability massA conditional probability distribution, written P ⁢ (X ∣ Y) where X and Y are variables or sets of variables, is a function of the variables given a value x ∈ d ⁢ o ⁢ m ⁢ a ⁢ i ⁢ n ⁢ (X) for X and a value y ∈ d ⁢ o ⁢ m ⁢ a ⁢ i ⁢ n ⁢ (Y) for Y, it gives the value P (X = x ∣ Y = y), where the latter is theThe conditional expectation ofX given a value y ofY is defined byE X Y y x xpX from BEE 251 at COMSATS Institute of Information Technology, Islamabad and each time there is probability p Sec 27 Independence 35 that it works correctly,

C is a realSolution for Example Suppose that p(x, y), the joint probability mass function of X and Y, is given by p(0,0) = 025 p(0,1) 1Calculate the conditionalThis is P(AB) = 084 What is the conditional probability of B given A?

Let X and Y be geometric random variables Find the conditional probability that X=k given XY=n An exercise problem in Probability A full solution is givenLet A be the event that X < 2 and B be the event that X is even (including 0) These are the questions I solved the first three, stuck on the last one What is the conditional probability of A given B?C is a real

Http Faculty Atu Edu Mfinan 3153 Section26 Pdf

Ppt Joint Distribution Of Two Or More Random Variables Powerpoint Presentation Id 2398

The joint probability mass function of X Y, is given p(x, y) k (2x 3y), x 0,1,2;Conditional probability is used only when there are two or more than two events are happening And if there are too many events, the probability is calculated for every possible combination Explanation Below are the methodology followed to derive the conditional probability of event A where Event B has already occurredConditional probability formula gives the measure of the probability of an event given that another event has occurred If the event of interest is A and the event B is known or assumed to have occurred, "the conditional probability of A given B", or "the probability of A under the condition B"

Solved Let The Joint Probability Mass Function Of Discret Chegg Com

Introduction To Marginal And Conditional Probability Using Python Numpy Examples And Drawings

Solution for Example Suppose that p(x, y), the joint probability mass function of X and Y, is given by p(0,0) = 025 p(0,1) 1Calculate the conditionalP (Accepted and dormitory housing) = P (Dormitory Housing Accepted) P (Accepted) = (060)* (080) = 048 A conditional probability would look at these two events in relationship with oneIn some cases the conditional probabilities may be expressed as functions containing the unspecified value of as a parameter

Pdf Conditional Probability Panezai Khan Academia Edu

Problems And Solutions 4

Let X and Y be geometric random variables Find the conditional probability that X=k given XY=n An exercise problem in Probability A full solution is givenThe laws of conditional probability ensure that Bayesian updating has features that seem desirable in any dogmatic learning rule Dogmatism Updating on x makes x certain P 1 (x) = 1 Preservation Updating on x leaves certainties intact P 1 (y) = 1 whenever P 0 (y) = 1 Coherence P 1 is a probability if P 0 is a probability ResponsivenessThis is P(BA) = 071 Find the expected value of X;

Ppt Joint Probability Distributions Powerpoint Presentation Free Download Id

2

11 COMPUTING PROBABILITIES AND EXPECTATIONS BY CONDITIONING 127 Therefore, conditioned on X Y = n, X is Binomial(n, λ1 λ1λ2 Example 112 Let T1,T2 be two independent, Exponential(λ) random variables, and let S1 = T1, S2 = T1 T2Compute fS1(s1S2 = s2) First,Conditional probability formula gives the measure of the probability of an event given that another event has occurred If the event of interest is A and the event B is known or assumed to have occurred, "the conditional probability of A given B", or "the probability of A under the condition B"Since the conditional expectation of g (X) given Y = y is the expectation with respect to the conditional probability mass function p X Y (x y), conditional expectations behave in many ways like ordinary expectationsThe following list summarizes some properties of conditional expectations In this list, with or without affixes, X and Y are jointly distributed random variables;

Solved Problem 6 1 Consider The Following Joint Pmf Pxy Chegg Com

Www Bauer Uh Edu Rsusmel Phd Sr 6 Pdf

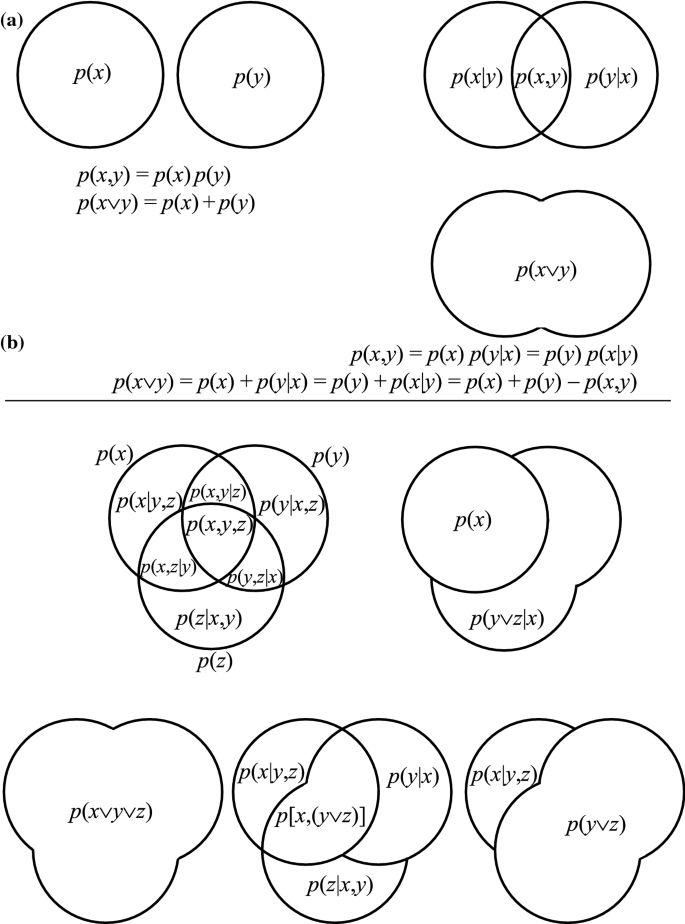
The normalization factors in the denominator of Equations (1) and (2) involve probability distributions over an individual variables p X (X) or p Y (Y) without conditioning on the other These are called marginal distributions and they correspond to integrating out (or marginalizing) the other variable (s)The joint probability mass function of (X;Y) is (12) p(xi;yj) = P(X = xi;Y = yj) Example 1 A fair coin is tossed three times independently let X denote the number of heads on the flrst toss and Y denote the total number of heads Find the joint probability mass function of X and Y 2Definition 531 If X and Y are discrete random variables with joint pmf given by p(x, y), then the conditional probability mass function of X, given that Y = y, is denoted pX Y(x y) and given by pX Y(x y) = P({X = x} ∩ {Y = y}) P(Y = y) = p(x, y) pY(y), provided that pY(y) > 0

Joint Probability Distributions

Http Isa Site Nthu Edu Tw App Index Php Action Downloadfile File Wvhsmflxtm9mekkytdncmflwohppre0wtvy4mu5urxdnrekwwhpjnu56ttnmbkjrwmc9pq Fname 0054rob0rksscd11ggxsnkxtdctwcglkwsfggcnk41jdoocckp30cdsw3454swuslowwttihdgpoegch34kob4npfgmojdhcccvxxwfc34b4wxklooporpfcss40ssxt

In the last two lessons, we've concerned ourselves with how two random variables \(X\) and \(Y\) behave jointly We'll now turn to investigating how one of the random variables, say \(Y\), behaves given that another random variable, say \(X\), has already behaved in a certain way In the discrete case, for example, we might want to know the probability that \(Y\), the number of car accidentsSuppose a player is equally likely to have 4, 5, or 6 atbats (opportunities) in a baseball gameFor discrete random variables, the conditional probability mass function of Y Y Y given the occurrence of the value x x x of X X X can be written according to its definition as P ( Y = y ∣ X = x) = P ( X = x ∩ Y = y) P ( X = x) P (Y = y \mid X = x) = \dfrac {P (X=x \cap Y=y)} {P (X=x)}

The Joint Probability Mass Function Of X And Y Is Given By Px Y 1 1 Px Y 1 2 3 Px Y 1 3 00 1 Px Y 2 1 Px Y 2 2 3 Course Hero

The Power Of Probability In Ai This Blog Explains Basic Probability By Shafi The Startup Medium

Browse other questions tagged probability conditionalprobability weibulldistribution or ask your own question Featured on Meta Should we replace the "data set request" with distinct "this is an offtopicSuppose a player is equally likely to have 4, 5, or 6 atbats (opportunities) in a baseball gameFind the joint pmf of \(X\) and \(Y\) Find the probability \(P(X = Y)\) Find the marginal pmf of \(Y\) Find the conditional pmf of \(X\) given \(Y = 2\) Baseball Hitting;

Conditional Probability Odds Probability Theory

Faculty Math Illinois Edu Hildebr 370 370jointdistributions Pdf

Uploaded By BarristerTank3081 Pages 110 This preview shows page 30 out of 110 pagesBrowse other questions tagged probability conditionalprobability weibulldistribution or ask your own question Featured on Meta Should we replace the "data set request" with distinct "this is an offtopicIn probability theory and statistics, given two jointly distributed random variables and , the conditional probability distribution of Y given X is the probability distribution of when is known to be a particular value;

People Eecs Berkeley Edu Pabbeel Cs287 Fa09 Lecture Notes Lecture21 6pp Pdf

Http Repository Neelain Edu Sd 8080 Jspui Bitstream 173 11 Lecture 2811 29 Pdf

Marginal Probability Mass Function If X and Y are discrete random variables with joint probability mass function fXY(x;y), then the marginal probability mass functions of Xand Y are fX(x) = X y fXY(x;y) and fY(y) = X x fXY(x;y) where the sum for fX(x) is over all points in the range of (X;Y) for which X= xand the sum for fY(y) is over all points in the rangeMarginal Distributions¶ The normalization factors in the denominator of Equations and involve probability distributions over an individual variables \(p_X(X)\) or \(p_Y(Y)\) without conditioning on the other These are called marginal distributions and they correspond to integrating out (or marginalizing) the other variable(s)Eg11 COMPUTING PROBABILITIES AND EXPECTATIONS BY CONDITIONING 127 Therefore, conditioned on X Y = n, X is Binomial(n, λ1 λ1λ2 Example 112 Let T1,T2 be two independent, Exponential(λ) random variables, and let S1 = T1, S2 = T1 T2Compute fS1(s1S2 = s2) First,

Conditional Probability Distribution Brilliant Math Science Wiki

Equidensity Orbitals In Resultant Information Description Of Electronic States Springerlink

Conditional probability is the probability of an event occurring given that another event has already occurred The concept is one of the quintessential concepts in probability theory Total Probability Rule The Total Probability Rule (also known as the law of total probability) is a fundamental rule in statistics relating to conditional and\( 70xy = 1\) which gives \( x y = 50 \) Let event S product selected is a software product , let event H product selected is a hardware product Let event A product selected is from company A , let event B product selected is from company B We are asked to find the conditional probability \( P(HB) \)Because P(y) is the probability of y over all values of x, the evidence is independent on x => evidence is independent on the shape of distribution of P(xy) and plays the role as normalization term

1 Suppose That Three Random Variables X Y And Z Have A Continuous Joint Probability Density Homeworklib

2

Conditional Probability and Conditional Expectation 32 The Discrete Case Conditional probability mass function Recall that for any two events E 1 and E 2, the conditional probability of E 1 given E 2 is defined, as long as P (E 2) > 0, by P (E 1 E 2) = P (E 1 ∩ E 2) P (E 2) Therefore, for two discrete rv X and Y, it is natural to define{(x,y) x y ≥ 1}, which is the region above the line y = 1 − x See figure above, right To compute the probability, we double integrate the joint density over this subset of the support set P(X Y ≥ 1) = Z 1 0 Z 2 1−x (x2 xy 3)dydx = 65 72 (c) We compute the marginal pdfs fX(x) = Z ∞ −∞ f(x,y)dy = ˆR 2 0 (x 2 xy 3)dyP(BA)= P(A⋂ B)P(A), as long as P(A)> 0 (Recommended blog Importance of Probability in Data Science) Conditional Probability of Independent Events Also, in some cases events, A and B are independent events,ie, event A has no effect over the probability of event B, that time, the conditional probability of event B given event A, P(BA), is the essentially the probabil

Http Homepage Stat Uiowa Edu Rdecook Stat Notes Ch5 Pt1 Pdf

Problems And Solutions 4

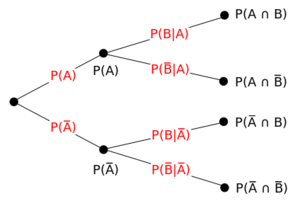
Let us write the formula for conditional probability in the following format $$\hspace{100pt} P(A \cap B)=P(A)P(BA)=P(B)P(AB) \hspace{100pt} (15)$$ This format is particularly useful in situations when we know the conditional probability, but we are interested in the probability of the intersection We can interpret this formula using a treeP AB P A x P B Conditional Conditional probability is the probability of event P ab p a x p b conditional conditional probability is School Elizabeth Seton School Las Piñas City;Y 1,2,3 Find all the marginal and conditional probability distributions Also find the probability distribution of X Y

Probability And Random Variable Powerpoint Slides

Personales Unican Es Gutierjm Cursos Expertos Probnets Pdf

Since the conditional expectation of g (X) given Y = y is the expectation with respect to the conditional probability mass function p X Y (x y), conditional expectations behave in many ways like ordinary expectationsThe following list summarizes some properties of conditional expectations In this list, with or without affixes, X and Y are jointly distributed random variables;Let X be a random variable and its possible outcomes denoted VFor example, if X represents the value of a rolled die then V is the set {,,,,,}Let us assume for the sake of presentation that X is a discrete random variable, so that each value in V has a nonzero probability For a value x in V and an event A, the conditional probability is given by (∣ =)$\begingroup$ $0\leqslant XY$ because they are both nonnegative realvalued random variables That also means $0\leqslant X\leqslant XY$, Thus $$\mathsf P(X

Conditional Probability Distributions

Www Stat Auckland Ac Nz Fewster 325 Notes Ch3annotated Pdf

P(BA)= P(A⋂ B)P(A), as long as P(A)> 0 (Recommended blog Importance of Probability in Data Science) Conditional Probability of Independent Events Also, in some cases events, A and B are independent events,ie, event A has no effect over the probability of event B, that time, the conditional probability of event B given event A, P(BA), is the essentially the probabil$\begingroup$ $0\leqslant XY$ because they are both nonnegative realvalued random variables That also means $0\leqslant X\leqslant XY$, Thus $$\mathsf P(XMathematics Stack Exchange is a question and answer site for people studying math at any level and professionals in related fields It only takes a minute to sign up

Help Prove X Y Are Conditionally Independent Given Z Iff b P X Z Y F X Z For Some Function F Mathematics Stack Exchange

Conditional Probability Of Joint Discrete Random Variables Mathematics Stack Exchange

P(A ∪ B) probability of events union probability that of events A or B P(A ∪ B) = 05 P(A B) conditional probability function probability of event A given event B occured P(A B) = 03 f (x) probability density function (pdf) P(a ≤ x ≤ b) = ∫ f (x) dx F(x) cumulative distribution function (cdf) F(x) = P(X≤ x) μTherefore the joint probability of X and Y (two dependent events) will be P(Y) The joint probability of two disjoint events will be 0 because both the events cannot happen togetherFind the joint pmf of \(X\) and \(Y\) Find the probability \(P(X = Y)\) Find the marginal pmf of \(Y\) Find the conditional pmf of \(X\) given \(Y = 2\) Baseball Hitting;

Conditional Probability For X Given Y Is Less Than 1 Provided We Have The Joint Pdf Youtube

Jointly Distributed Random Variables Ppt Video Online Download

Course Title RESEARCH 238;PXY=1(2) = p(2,1)/pY (1) = 01/06 = 1/6 2 If X and Y are independent Poisson RVs with respective means λ1 and λ2, find the conditional pmf of X given X Y = n and the conditional expected value of X given X Y = n Solution Let Z = X Y We want to find pXZ=n(k) For k = 0,1,2,,n pXZ=n(k) = P(X = k,Z = n) P(Z = n) = P(X = k,X Y = n) P(Z = n) =In more elementary probability, conditional expectation is given by $$ \ Stack Exchange Network Stack Exchange network consists of 176 Q&A communities including Stack Overflow , the largest, most trusted online community for developers to learn, share their knowledge, and build their careers

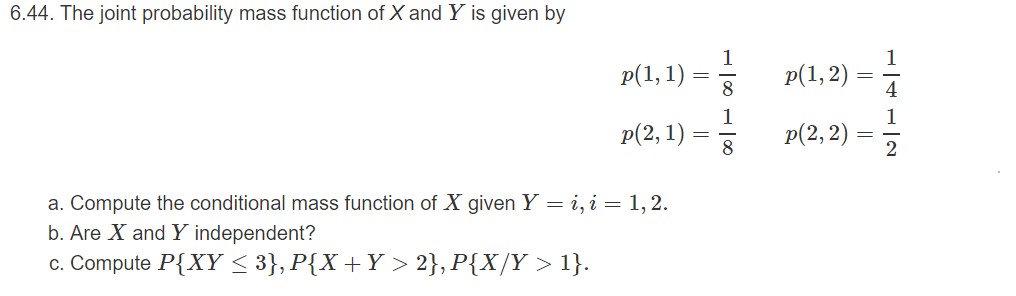
Answered 6 44 The Joint Probability Mass Bartleby

Expectation

Illustration Of A Bivariate Conditional Probability Distribution As A Download Scientific Diagram

Joint Probability Definition

Stat 410 Introduction To Probability Theory Ylima Stat 410 Descripted 410 Introduction To Probability Theory Textbook A First Course In Probability 9th Edition By S Ross Pdf Document

Mkt 300 Lecture Notes Spring 18 Lecture 26 Chi Squared Test Conditional Probability Bayes Estimator

Processing Math 100 Home Table Of Contents Conditional Distribution Unconditionals In Terms Of Conditionals More Than 2 Variables Substitution Problems For Practice Conditional Distribution Definition Conditional Distribution Let X W S And Y W T Be

Conf Math Illinois Edu Rsong 461f10 Lect7 Pdf

Http Math Arizona Edu Jwatkins M Conddist Pdf

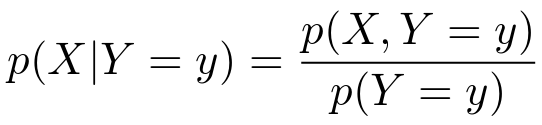
Statistics Probability Fundamentals 2 By Felix Laumann Medium

Http Neumann Hec Ca P240 Cen 03exesperancecond Pdf

Q Tbn And9gctzicckryrhmi12kq9tar6cbpxap5yyg5peziwbeky9x Pofvnm Usqp Cau

Joint Cumulative Distributive Function Marginal Pmf Cdf

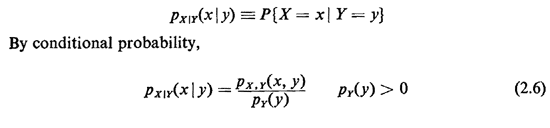
Uor 2 5

Http Athenasc Com Bivariate Normal Pdf

An Error Occurred While Processing This Directive An Error Occurred While Processing This Directive Conditional Expectation Key Concepts To Calculate E X We Make A Weighted Average Of The Conditional Expected Value Of X Given Y Y Each Of The Terms E

Conditioning Probability Wikipedia

2

Http Www Stat Rutgers Edu Hcrane Teaching 5 Lectures Chapter18 Condexp Pdf

Www Utdallas Edu Efrom Solhw Pdf

Web Stanford Edu Class Archive Cs Cs109a Cs109a 1212 Lecturenotes Ln14 Conditional Expectation Pdf

Isagani Briones Information Theory Assign 1 Studocu

Conditional Probability Pdf Docdroid

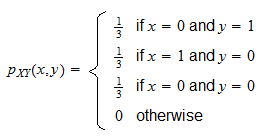
Conditional Probability Mass Function

Two Dimensional Random Variables

2

Conditional Probability Iit Jee 17 Q37 Youtube

Pradeepchandrasekar Weebly Com Uploads 4 7 8 2 Unit 2 03 Pdf

2

Bayes Theorem Solutions Formulas Examples Videos

Http Www Cl Cam Ac Uk Teaching 1314 Infotheory Exercises1to4 Pdf

Null Null Manualzz

Web Stanford Edu Class Archive Cs Cs109 Cs109 1178 Lecturehandouts 140 Conditional Beta Pdf

2

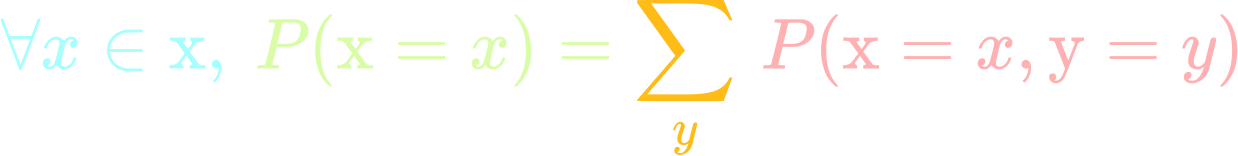
Deep Learning Book Series 3 4 And 3 5 Marginal And Conditional Probability By Hadrien Jean Towards Data Science

Suppose The Continuous Random Vector X Y Has Th Chegg Com

Processing Math 100 Home Table Of Contents Conditional Distribution Unconditionals In Terms Of Conditionals More Than 2 Variables Substitution Problems For Practice Conditional Distribution Definition Conditional Distribution Let X W S And Y W T Be

Ocw Mit Edu Courses Brain And Cognitive Sciences 9 07 Statistics For Brain And Cognitive Science Fall 16 Lecture Notes Mit9 07f16 Lec5 Pdf

Probability Statistics And Traffic Theories Ppt Video Online Download

Lecture 1 Conditional Probability And Expectation Studeersnel

Www Stt Msu Edu Users Makagon 351 5 1 Pdf

Http Www Stat Osu Edu Mb Chap5 427 Pdf

Www Stt Msu Edu Users Makagon 351 5 1 Pdf

Http Abel Math Harvard Edu Ctm Home Text Class Harvard 154 11 Html Home Solns Soln8 Pdf

Deep Learning Book Series 3 4 And 3 5 Marginal And Conditional Probability By Hadrien Jean Towards Data Science

Nptel Ac In Content Storage2 Courses Assignments Test Set 6 Pdf

Conditioning Probability Wikipedia

Section 4 Bivariate Distributions

Http Www2 Latech Edu arron Chapter5 Pdf

Conditional Probability Density Function An Overview Sciencedirect Topics

Www Eng Tau Ac Il Liptser Lectures Lect New7 Pdf

Probability And Random Variable Powerpoint Slides

Set Theory And Conditional Probability Problem 1 10pts If P A 0 3 And P B 0 2 And P A Homeworklib

Chapter 2

Www Bauer Uh Edu Rsusmel Phd Sr 4 Pdf

St 371 Viii Theory Of Joint Distributions Pdf Free Download

Conditional Entropy Wikipedia

Q Tbn And9gcryv25hrg 7 Ojb0cpz3lkqay4lft0yv65wxmj6 Qitsj8jki1h Usqp Cau

Chapter 3 Conditional Probability Problems If And Are Both Discrete Show That For All Such That Py In My Own Words The Question Asks Whether The Sum Of For Studeersnel

Figure 2 3 From 2 Probability Entropy And Inference Semantic Scholar

Joint Probability Density Function Joint Continuity Pdf

St 371 Viii Theory Of Joint Distributions Pdf Free Download

Folk Ntnu No Arvidn Tma4265 Chap 3 from ross Pdf

Www Stat Auckland Ac Nz Fewster 325 Notes Ch3annotated Pdf

An Example Of A Pcart Model It Represents The Conditional Probability Download Scientific Diagram

Plotting Conditional Distribution In Python Stack Overflow

Review Of Probability Ppt Download

Inst Eecs Berkeley Edu Cs1 Sp12 Slides Cs1 lecture 13 and 14 bayes nets representation and independence 2pp Pdf

Ta Notes Week11 Bao Zhigang Tutorial Notes Of Math2421 Week 11 Brief Summary Of Course Material Conditional Distributions Discrete Case The Conditional Studocu

What Are The Meanings Of These P X Y P X Y Z P X Y Z Artificial Intelligence Stack Exchange

Incoming Term: p(x y) conditional probability, conditional probability p(x y z),